Défi du jour, bonjour ! Le Captain', joueur professionnel de Ligue 1 après son passage raté dans le monde de l'économie, a durant la saison 2012/2013 marqué 5 buts sur un total de 15 tirs, effectué 4 passes décisives, reçu 4 cartons rouges et 8 jaunes (dur sur l'homme le Captain'), joué 36 matchs et commis 45 fautes pour 20 fautes subies. Avec toutes ces infos, déterminer à quel poste évolue le Captain' (gardien, défenseur, milieu, attaquant). Vous avez 2 heures ! A part si vous ne connaissez absolument rien au milieu du football, vous pouvez d'ores et déjà supprimer la classe "gardien" ; la probabilité qu'un gardien marque 5 buts et effectue 4 passes décisives sur une année est très proche de 0. Mais entre les trois autres classes, il peut y avoir débat. Alors comment déterminer le poste du Captain' ? Méthode #1 : la combo feeling+chance. Bon sympa, mais ça va pas faire un super article tout ça. Méthode #2 : la classification naïve bayésienne supervisée. Pas de panique, c'est finalement pas si compliqué que cela (tout est relatif...) !
 Mais quel est le lien avec l'économie ou la finance ? En finance, la méthode de classification naïve bayésienne supervisée est souvent utilisée afin de faire de l'analyse sémantique de texte, pour définir automatiquement si une suite de mots (articles, rapports, communiqués, tweets...) est plutôt optimiste, neutre ou pessimiste. L'idée est ensuite de voir l'impact que cela peut avoir sur les marchés financiers. Cette méthode permet de gagner du temps (classer à la main des milliers de textes peut amener rapidement au suicide) et ne fait pas intervenir la subjectivité ou le jugement du chercheur. L'inconvénient étant que ça déconne dans certains cas, par exemple pour gérer l'ironie ou le sarcasme. Dans le cadre de sa thèse, le Captain' avait besoin de revoir quelques notions à ce propos, et quoi de mieux pour se replonger dedans que de réaliser un petit projet concret sur un domaine "fun" (enfin "fun" pour un thésard) : le monde du football.
Mais quel est le lien avec l'économie ou la finance ? En finance, la méthode de classification naïve bayésienne supervisée est souvent utilisée afin de faire de l'analyse sémantique de texte, pour définir automatiquement si une suite de mots (articles, rapports, communiqués, tweets...) est plutôt optimiste, neutre ou pessimiste. L'idée est ensuite de voir l'impact que cela peut avoir sur les marchés financiers. Cette méthode permet de gagner du temps (classer à la main des milliers de textes peut amener rapidement au suicide) et ne fait pas intervenir la subjectivité ou le jugement du chercheur. L'inconvénient étant que ça déconne dans certains cas, par exemple pour gérer l'ironie ou le sarcasme. Dans le cadre de sa thèse, le Captain' avait besoin de revoir quelques notions à ce propos, et quoi de mieux pour se replonger dedans que de réaliser un petit projet concret sur un domaine "fun" (enfin "fun" pour un thésard) : le monde du football.
Première étape avant même de voir ce qu'est la classification naïve bayésienne : créer une base de données regroupant des statistiques sur l'ensemble des joueurs de foot de Ligue 1. Hop on ouvre Excel, on fait petit tour sur internet et on synthétise tout cela dans un beau tableau, avec bien évidemment en dernière colonne le poste du joueur. Cela nous donne donc quelques chose comme cela (avec au total les stats pour les 267 joueurs de ligue 1 ayant joué au minimum 20 matchs) :

Ensuite, on importe toutes ces données dans un logiciel de stats ou d'économétrie (personnellement j'utilise "R", logiciel gratuit pour Mac/Windows), et on peut commencer à faire quelques graphiques histoire de voir, selon le poste, si des caractéristiques ressortent. Il est possible de remarquer ici que pour certaines caractéristiques, des groupes se forment en fonction des postes (les défenseurs sont avec les défenseurs, les attaquants avec les attaquants). Par exemple, en ce qui concerne le nombre de buts, les attaquants (points rouges) ont tendance à se regrouper (+ de buts que les autres postes), tandis qu'en ce qui concerne les fautes commises, les gardiens (points jaunes) se regroupent (peu de fautes commises par les gardiens). Assez logique tout cela.
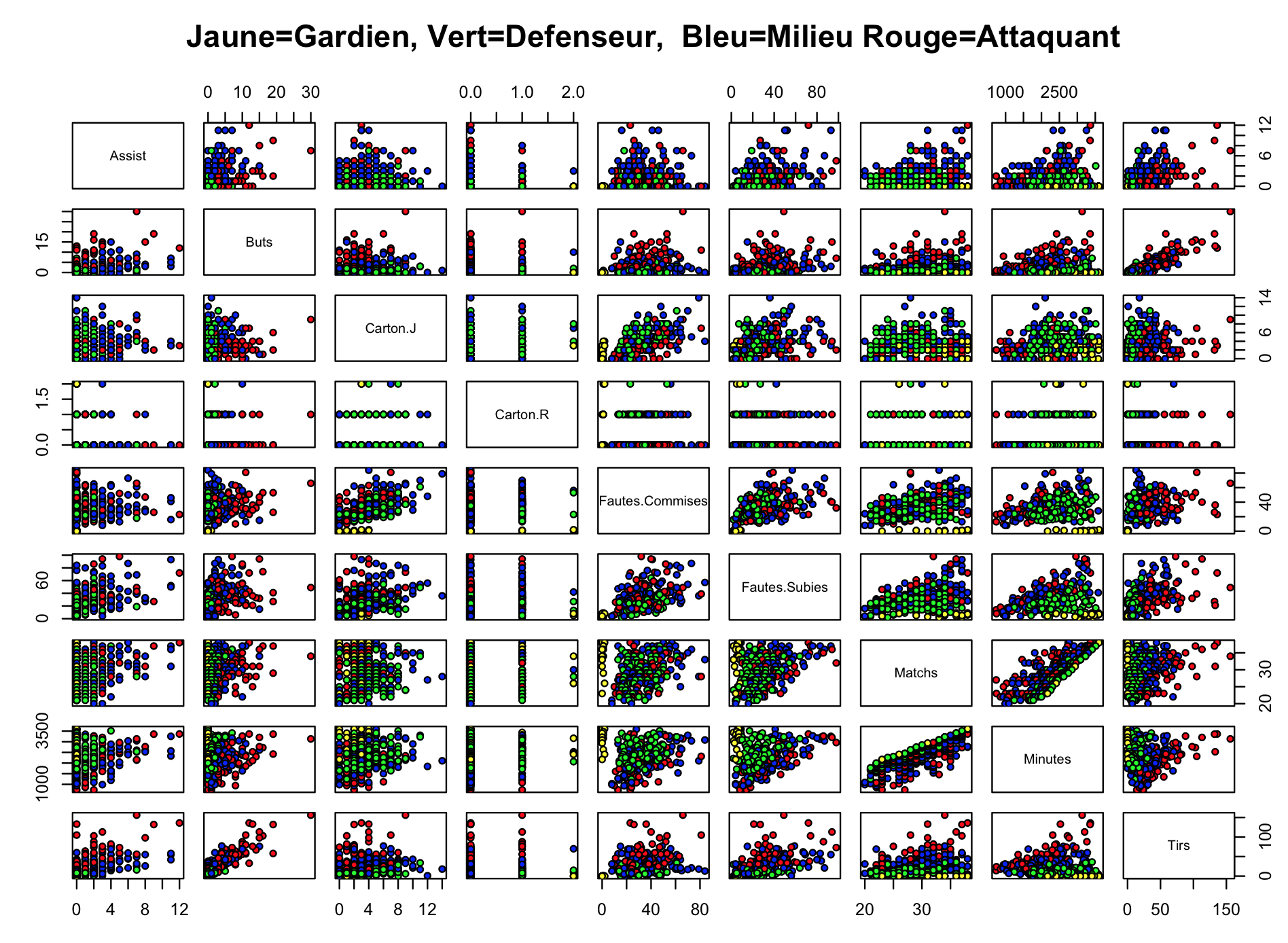
Cette matrice est simplement à titre informatif, car justement dans le cadre de la classification naïve bayésienne, on considère chacun des attributs comme indépendant. C'est d'ailleurs pour cela que cette classification est appelée "naïve". Même si ces caractéristiques sont liées dans la réalité, un classifieur bayésien naïf déterminera qu'un joueur est un attaquant en considérant indépendamment ses caractéristiques de buts, de passes décisives, de fautes subies... Il est bien évidemment possible d'introduire certaines relations de dépendance, avec l'utilisation par exemple d'un ratio "buts/passes décisives", mais ici on restera dans un exemple simple.
Bref, revenons en à notre classification. Pour chacune des caractéristiques, l'idée est donc de voir la probabilité qu'un joueur évolue à un certain poste étant donné la valeur de cette caractéristique. Il s'agit alors de probabilités conditionnelles, par exemple la probabilité qu'un joueur soit gardien, défenseur, milieu ou attaquant en sachant qu'il a marqué 12 buts cette saison (avec la somme des probabilités conditionnelle égale à 1). Pour chacune des caractéristiques, la probabilité d'appartenance à une classe dépend de la moyenne et de l'écart-type de cette classe. Si l'on prend l'exemple pour le nombre de buts, sur notre échantillon, un attaquant a en moyenne marqué 4,72 buts avec un écart-type de 5,21 (c'est à dire de fortes variations entre les attaquants, certains à 0 buts et Zlatan à 30 buts), tandis qu'en ce qui concerne les gardiens, la moyenne est de 0,03 buts avec un écart-type très faible de 0,17 (le seul gardien à avoir marqué 1 but étant Ali Ahamada). Pour cette caractéristique, un joueur ayant marqué 0 buts sur la saison aura donc une probabilité bien supérieure d'être classifié comme gardien plutôt que comme attaquant (même s'il est possible qu'un attaquant ne marque pas de la saison). Un autre exemple : en ce qui concerne la caractéristique fautes subies, il est possible de déterminer les lois de probabilités pour chacune des classes, et de faire un beau graphique qui nous donne ça:
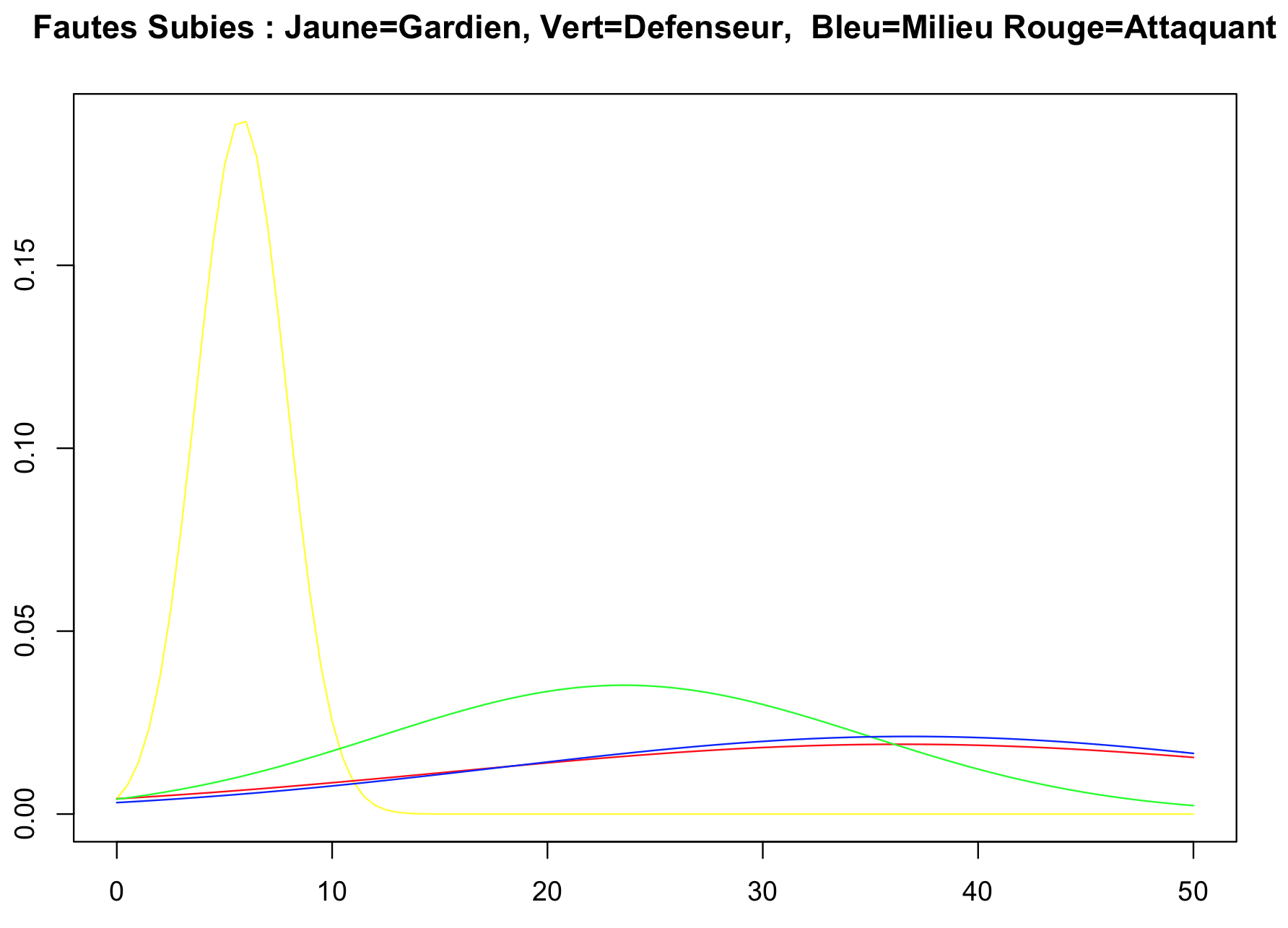
En ce qui concerne cette caractéristique, un joueur ayant subi 5 fautes sur la saison aura donc une plus forte probabilité d'être gardien qu'un autre poste. Par contre, il est très difficile de différencier un milieu (en bleu) d'un attaquant (en rouge) en utilisant seulement cette caractéristique.
Avec l'aide d'un logiciel statistique (ça peut se faire à la main, mais c'est long), il est donc possible de calculer l'ensemble des probabilités conditionnelles de toutes les caractéristiques en fonction de chaque poste. Voici la recette en quatre étapes :
Etape 1 : Avec la commande "classifier<-naiveBayes(foot[,3:11], foot[,12])", déterminer pour chaque caractéristique (colonne 3 à 11) les lois de probabilité pour chaque classe (la 12ème colonne de notre tableau).
Etape 2 : Créer un fichier Excel comportant les individus à classifier, en remplissant les caractéristiques pour chacun des joueurs, sans indiquer le poste bien évidemment (c'est la variable que l'on cherche à déterminer). Dans le tableau ci-dessous, on retrouve donc Le Captain' avec les caractéristiques indiquées en introduction, avec quatre autres joueurs "tests".

Etape 3 : Demander à votre nouveau copain "R" de prévoir la classe en fonction des probabilités conditionnelles, avec la commande "predict(classifier, foot_t)" ("foot_t" regroupant la liste des joueurs à tester).
Etape 4 : Regarder les résultats et conclure. Sous "R", vous obtenez alors en réponse à cette commande la liste "D A M D G", signifiant donc que le premier joueur (le Captain') est classifié comme défenseur, le second (le Buteur) comme attaquant, le troisième (le ZZ) comme milieu, le quatrième (le Rock) comme défenseur et le dernier (le Wall) comme gardien. Cela fonctionne donc plutôt bien ; les quatres autres joueurs "tests" ayant des caractéristiques volontairement prononcées pour tester le modèle de classification.
![]()
Conclusion : Mes excuses aux "puristes" de la statistique ; c'est ici un article de vulgarisation avec pas mal de raccourcis, mais pour la bonne cause ! Il est possible d'améliorer fortement la classification ci-dessus, en ajoutant des variables ou en retravaillant les variables existantes (pour normaliser par le nombre de minutes jouées par exemple). Le Captain' est ici classifié comme Défenseur non pas via son nombre de buts ou de passes décisives qui ressemblent en moyenne davantage aux statistiques d'un milieu ou d'un attaquant, mais en raison de son faible nombre de fautes subies et de son nombre de tirs très largement en dessous de la moyenne d'un attaquant (54 tirs) ou d'un milieu (30 tirs). Si vous avez envie de classer des fleurs plutôt que des footballeurs, suivez le tuto par ici ("Introduction to Artificial Intelligence (ARIN) - Naive Bayes with R").
 Cet article est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas de Modification 4.0 International. N'hésitez donc surtout pas à le voler pour le republier en ligne ou sur papier.
Cet article est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas de Modification 4.0 International. N'hésitez donc surtout pas à le voler pour le republier en ligne ou sur papier.