"Dis moi ce que tu cherches, et je te dirai comment le trouver". L'exploration de données ou le "data-mining" consiste, à partir d'un grand nombre de données, à identifier des relations de corrélation ou de causalité entre différentes variables. Par exemple, supposons que vous ayez une base de données de séries temporelles diverses et variées (taux d'intérêt, taux de change, prix du baril de pétrole, nombre de moutons en Irlande, poids moyen d'un bébé à sa naissance, production de beurre au Bangladesh ... et des centaines d'autres séries temporelles) et que vous ayez envie de voir quelles variables peuvent permettre d'expliquer les variations de la bourse américaine sur une période donnée. Pour cela, vous allez donc ouvrir un logiciel économétrique, indiquer votre variable dépendante (l'indice boursier S&P500 par exemple) ainsi que l'ensemble des variables explicatives (toutes les autres séries) et commencer à jouer un peu avec les données. Mais entre "jouer" avec des données et les "manipuler", il n'y a souvent qu'un pas qu'il ne faut pas franchir !
 C'est là la différence entre l'exploration de données (data-mining) et l'espionnage de données (data-snooping). Le problème est que l'espionnage de données vous permettra d'avoir des belles régressions qui fonctionnent sur votre échantillon et une belle histoire à raconter (même si cette histoire est fausse), comme l'a montré David Leinweber dans "Stupid Data Miner Tricks : Overfitting the S&P". En réalisant un grand nombre de régression pour expliquer la variation annuelle du S&P500 entre 1981 et 1993, David Leinweber a montré qu'une variable permettait d'expliquer 75% de la variance du S&P sur la période : la production de beurre au Bangladesh !
C'est là la différence entre l'exploration de données (data-mining) et l'espionnage de données (data-snooping). Le problème est que l'espionnage de données vous permettra d'avoir des belles régressions qui fonctionnent sur votre échantillon et une belle histoire à raconter (même si cette histoire est fausse), comme l'a montré David Leinweber dans "Stupid Data Miner Tricks : Overfitting the S&P". En réalisant un grand nombre de régression pour expliquer la variation annuelle du S&P500 entre 1981 et 1993, David Leinweber a montré qu'une variable permettait d'expliquer 75% de la variance du S&P sur la période : la production de beurre au Bangladesh !
Mais Captain', cela n'a aucun sens ! Non aucun, mais il faut bien comprendre trois choses : (1) les tests économétriques se font toujours en définissant un intervalle de confiance, ce qui signifie que lorsqu'une variable est significative, il est possible que cette significativité soit due au hasard (l'intervalle de confiance "standard" est de 95%) (2) plus l'échantillon est petit, plus le risque de trouver des relations "fallacieuses" est grand (ici seulement 13 points), (3) les coefficients d'une régression sont fallacieux si les variables ne sont pas stationnaires (il faudrait relier la variation annuelle du S&P avec la variation annuelle de la production de beurre).
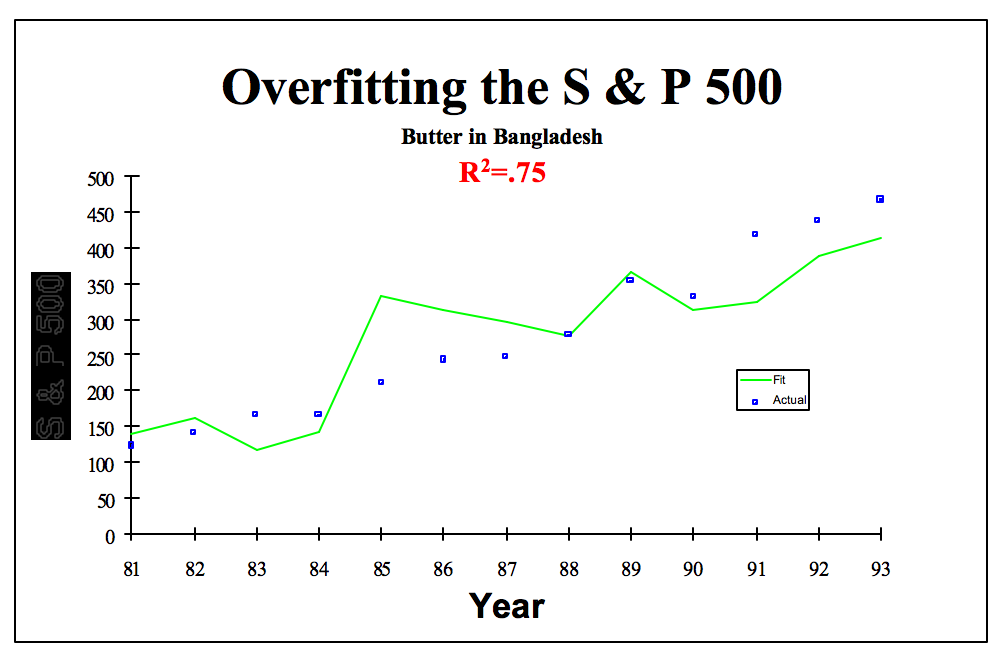
Sur le graphique ci-dessous, on voit bien que les estimations faites en utilisant la production de beurre au Bangladesh (courbe verte) sont assez proches du niveau réel du S&P (points bleus). Mais nous avons considéré ici une seule variable ! Il est assez facile de trouver une relation sur l'échantillon (in-sample) bien meilleure, en utilisant différentes techniques : (1) en combinant les variables entre elles (2) en considérant les retards des variables et (3) en utilisant des fonctions polynomiales (par exemple le carré de la production de beurre). Pour faire simple, au lieu d'estimer si le niveau du S&P est corrélé avec la production de beurre, vous allez voir le lien existant par exemple avec la racine cubique du nombre de moutons en Irlande, la variation du nombre de naissances prématurées et le logarithme de la production de beurre au Bangladesh...
En augmentant le nombre de modèles testés et en combinant/modifiant les variables à l'infini (et l'au delà), vous allez forcément à un moment ou à un autre trouver une relation significative entre votre variable dépendante et une combinaison linéaire ou non de variables explicatives. Par exemple, dans le cas du S&P, David Leinweber montre qu'une combinaison entre la production de beurre au Bangladesh et aux USA, la production de fromage aux USA et le nombre de moutons dans les deux pays permet d'expliquer 99% de la variance du S&P et d'obtenir un modèle quasi-parfait !
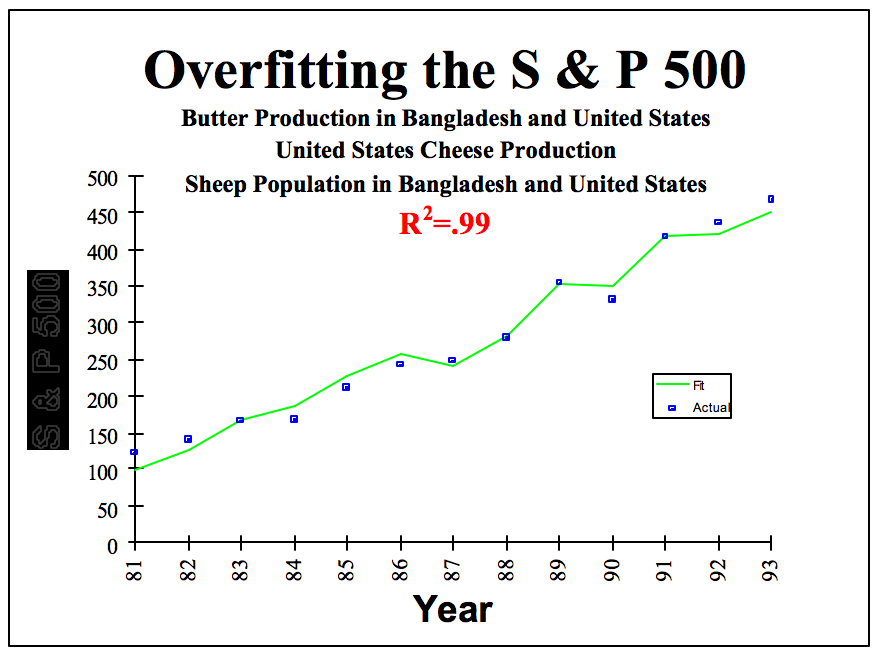
Dans cette situation, il est assez évident que cette relation est simplement le fruit du hasard et due à une exploration trop intensive des données. Mais imaginez qu'à la place de ces variables "folkloriques", le hasard ait choisi de montrer une forte relation entre le S&P500 et l'évolution de l'année précédente du carré du prix du pétrole et de la variation de la masse monétaire aux USA. Et bien là cette "fausse découverte" aurait sûrement été considérée avec plus d'attention ... à tort !
Mais comment éviter cela ? Premièrement, il faut veiller à ce que la taille de l'échantillon soit suffisante (à la louche une centaine de points minimum), ce qui a tendance à minimiser ce type d'erreur. Deuxièmement, il est important d'indiquer les différents modèles qui ont été testés, et non pas se concentrer uniquement sur le modèle qui a marché parmi les 50.000 modèles qui n'ont rien donné. Troisièmement, attention au régression fallacieuse lors de l'utilisation de variables temporelles en niveau (et non pas en variation ou différence première). Et quatrièmement, et c'est sûrement le plus important, il faut dans ce genre de situation réaliser un test "out-of-sample", c'est à dire estimer, en gardant la valeur des paramètres sur la période "in-sample" (ici de 1981 à 1993) si la relation existe toujours "out-of-sample" (par exemple sur la période 1994-1998). Bien souvent, des modèles qui ont l'air de donner quelquechose "in-sample" ne donne rien "out-of-sample", ce qui tend à montrer que la relation initiale était en fait biaisée ou simplement le fruit du hasard.
Conclusion : L'avalanche de données via le big-data et la hausse de la puissance de calcul permettent de tester plusieurs milliers de modèles avec des milliers de variables en un laps de temps très faible. Sur ces milllions de combinaisons, il y en a nécessairement une ou deux qui fonctionneront pas mal "in-sample" (variables significatives, R-squared élevé...) ! Mais rappelez vous alors ces deux citations de George Box, statisticien anglais : (1) "Statisticians, like artists, have the bad habit of falling in love with their models." et (2) "Essentially, all models are wrong, but some are useful". Après cela, réalisez un test "out-of-sample" et sortez des mouchoirs en voyant que finalement, encore une fois, votre modèle ne donne rien... Mais il est préférable de conclure que rien ne fonctionne avec les bons tests plutôt que de raconter une "fausse belle histoire" basée sur des erreurs méthodologiques.
 Cet article est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas de Modification 4.0 International. N'hésitez donc surtout pas à le voler pour le republier en ligne ou sur papier.
Cet article est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas de Modification 4.0 International. N'hésitez donc surtout pas à le voler pour le republier en ligne ou sur papier.











