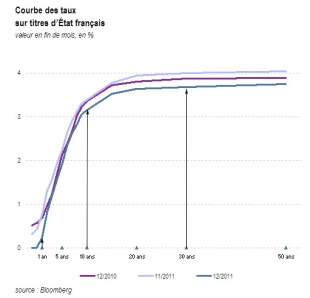
Pour éviter que la dette en % du PIB ne s'envole, on entend parler de pas mal de techniques (1) faire baisser les taux d'intérêts auxquels l'Etat emprunte, (2) augmenter le taux de croissance réel du pays, (3) recourir à l'inflation pour diminuer le poids de la dette et (4) rééquilibrer ou augmenter le solde budgétaire primaire, c'est à dire les recettes moins les dépenses de l'Etat, hors charges d'intérêts de la dette.
Mais quelles sont les relations entre ces différentes variables? Pour cela, nous allons faire un petit peu de mathématiques. Le taux d'endettement d'un pays à une date t est défini comme le ratio suivant (Dette en valeur € / PIB en valeur € ; relation (1) ). La dette en valeur a une date t va dépendre du montant de la dette l'année inférieure, du taux d'intérêt auquel l'Etat emprunte, et du déficit/excédent primaire réalisé par le pays au cours de l'année. Par exemple si un pays est endetté à hauteur de 100 milliards d'euros, qu'il emprunte au taux moyen de 5% et que pour l'année t, ce pays à eu un déficit budgétaire primaire de 10mds d'euros, sa dette à la fin de l'année sera de (100*1,05 + 10 = 115 mds d'euros):

Le PIB de l'année t en valeur est par définition égal au PIB de l'année (t-1) multiplié par (1 + le taux de croissance NOMINAL) (relation 3). En effet, il faut bien prendre en compte la croissance réelle et l'inflation, car l'on parle ici du PIB en valeur (prix courants) et non pas du PIB en volume (prix constants).
![]()
Bref, le taux d'endettement étant défini en (1), on peut donc poser, en divisant (2) par (3) et en posant c = tx de croissance nominal et SBP le Solde Budgétaire Primaire en valeur:
![]()
Or le ratio Dette en valeur (t-1) divisé par PIB en valeur (t-1) correspond au taux d'endettement en t-1, et le Solde Budgétaire Primaire en t divisé par le PIB valeur en t est l'exacte définition du solde budgétaire primaire en % du PIB en t, on arrive donc à l'équation (5):

Un petit tour de passe passe mathématique, et on trouvee donc à notre équation finale. Attention: il est possible de faire cette simplification uniquement si les valeurs de r et c sont très petites par rapport à 1, si ce n'est pas le cas (en gros si r ou c > à 10%) , l'estimation n'est pas très précise.

Cool ces calculs, mais on peut en faire quoi maintenant? Et bien nous venons de montrer mathématiquement comment les différentes variables influent sur le taux d'endettement. Pour réduire la dette en t, il faut donc soit (1) diminuer le taux d'intérêt, soit (2) augmenter le taux de croissance nominal (via croissance réelle ou inflation) et (3) avoir un solde budgétaire primaire élevé. C'est bien sympa, mais on le savait déjà tout ça Captain'!
Cette équation permet surtout de voir si la dynamique de la dette est stable ou instable. En effet, lorsque le taux d'intérêt (r) est supérieur au taux de croissance nominal (c), la dynamique du taux d'endettement devient instable, à moins que le pays n'ait un excédent budgétaire primaire élevé. C'est uniquement dans cette situation, lorsque la dynamique de la dette est instable (comme c'est le cas actuellement en Italie, Espagne, Grèce....) que la contrainte de solvabilité apparaît.
Conclusion: Si vous maîtrisez parfaitement cet article d'introduction au problème de la dynamique de la dette, le Captain' vous conseille de passer au niveau supérieur, en lisant l'article de Patrick Artus (Natixis) "L�€�apparition des contraintes de solvabilité : le choc pour les pays en difficulté de la zone euro". #MustRead
 Cet article est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas de Modification 4.0 International. N'hésitez donc surtout pas à le voler pour le republier en ligne ou sur papier.
Cet article est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas de Modification 4.0 International. N'hésitez donc surtout pas à le voler pour le republier en ligne ou sur papier.