Commençons avec trois questions posées par Valone & Tversky dans une étude publiée en 1985 dans le Journal of Cognitive Psychology : (1) "un basketeur ayant réussi ses deux derniers shoots a t-il plus de chance de marquer sur son prochain shoot qu'un basketeur ayant raté ses deux derniers tirs ?', (2) "est-il important de passer le ballon à un joueur "en réussite" ayant marqué sur ses deux derniers shoots?" et (3) "supposons un joueur marquant en moyenne sur 50% de ses tirs, quelle est sa probabilité de marquer s'il a réussi son dernier tir ?". Si vous avez répondu "oui" aux deux premières questions et "environ 60% de chance de marquer" à la troisième, alors vous avez répondu comme la majorité des américains sondés dans l'étude "The Hot Hand in Basketball: On the Misperception of Random Sequences" et vous adhérez donc à la "théorie de la main-chaude" : un joueur "on fire" (en confiance) ayant réussi ses derniers tirs aura plus de chance de marquer qu'un joueur ayant manqué ses derniers tirs. Et pourtant...
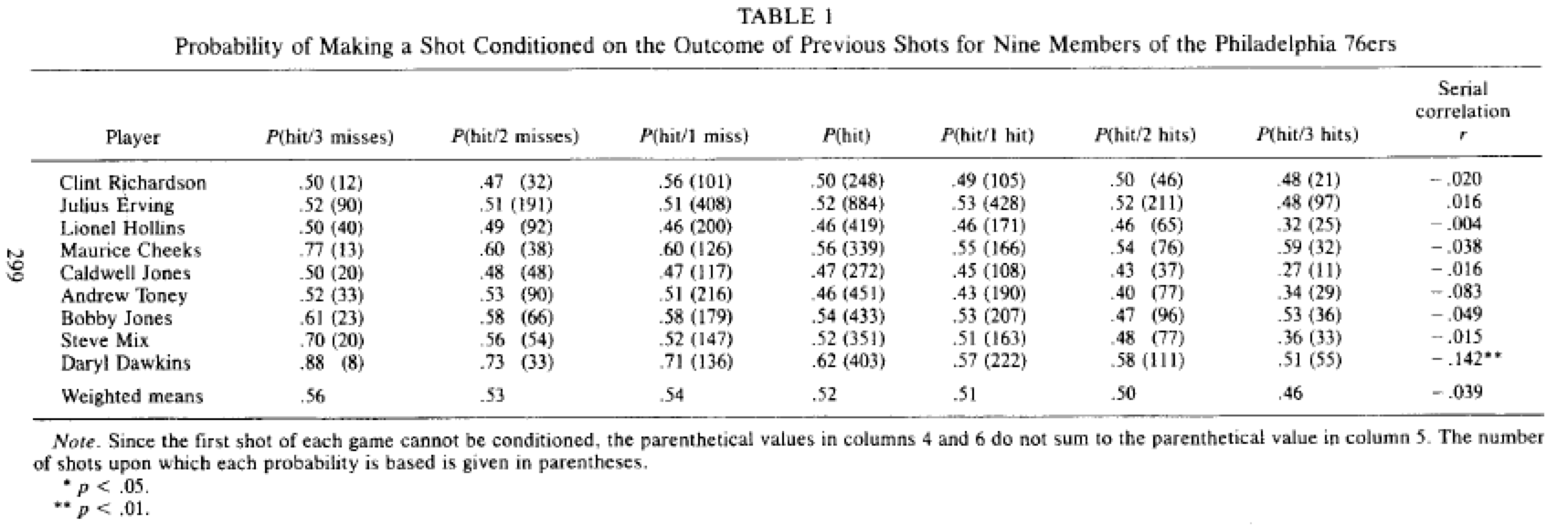
Dans l'étude citée précédemment, les deux chercheurs ont utilisé les statistiques individuelles de réussite de tous les joueurs des "Philadelphia 76ers" durant la saison 1980-1981. Pourquoi étudier cette équipe ? Simplement car à l'époque, Philadelphie était la seule équipe à collecter des statistiques détaillées sur ses joueurs, dont les séries de tirs réussis / manqués. D'un point de vue statistique, les chercheurs se sont donc intéressés à la probabilité conditionnelle de réussir un tir en fonction du résultat des tirs précédents, ainsi qu'à la corrélation du résultat des shoots (corrélation positive = si j'ai réussi mon tir avant, j'ai plus de chance de réussir le prochain). Dans cette équipe, la probabilité "non-conditionnelle" de réussir un shoot est de 52%. Lorsqu'un joueur a réussi son shoot précédent, la probabilité qu'il marque de nouveau est de 51%, tandis qu'elle est de 54% si le joueur a manqué son précédent shoot. En désaccord avec la théorie de la main chaude, la probabilité de marquer après 3 shoots réussis n'est que de 46%. De plus, pour chaque joueur (sauf pour Daryl Dawkins, qui réussi avec une proba de 88% après avoir raté 3 shoots... avec donc une corrélation négative de ses tirs), la différence n'est pas significative, ce qui implique une absence de main-chaude aussi au niveau individuel (et non pas uniquement au niveau agrégé).
Il est possible de trouver pas mal d'explications pour contredire ces résultats. Par exemple, un joueur est "on fire" peut avoir tendance à essayer des shoots plus difficiles, ce qui peut tendre à réduire logiquement sa probabilité de marquer (sans contredire la théorie de la main chaude). On pourrait aussi se dire que lorsqu'un joueur semble avoir la main chaude, la défense adverse fait davantage attention à ce joueur, ce qui va réduire sa probabilité de marquer sur son prochain shoot. Pour vérifier cela, nos deux chercheurs (P.S : Amos Tversky, l'un des deux chercheurs, a d'ailleurs beaucoup travaillé sur la théorie des perspectives avec Kahneman, prix Nobel d'Economie 2002... Décédé en 1996, Tversky n'a donc pas reçu le Prix Nobel) ont réalisé la même étude, mais en se basant uniquement sur les lancers francs afin d'enlever de nombreux biais possibles.
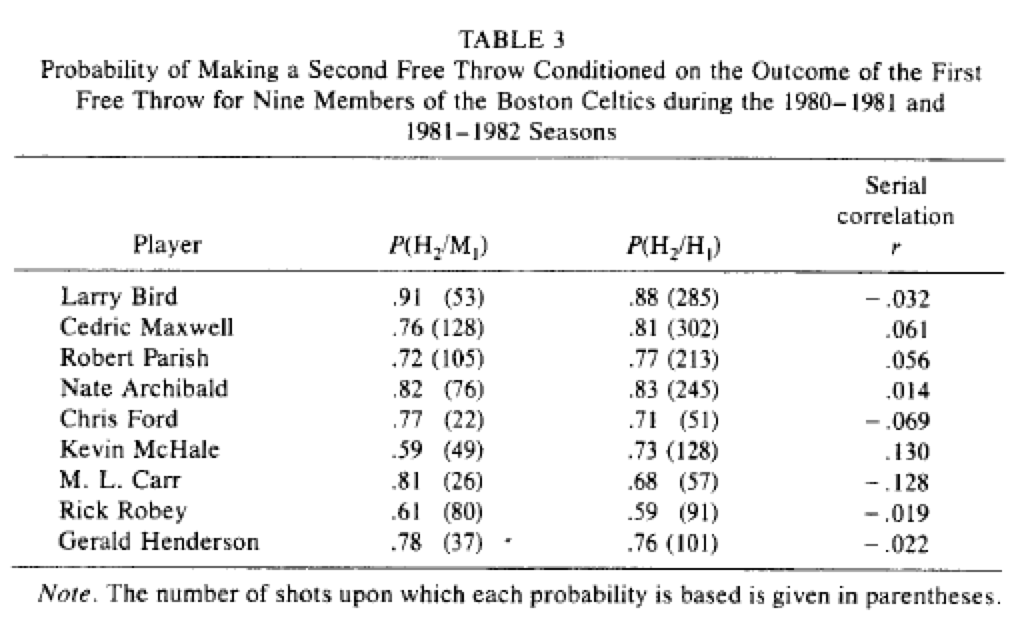
En regardant la probabilité de marquer le deuxième lancer franc en fonction de la réussite ou non du premier (probabilité conditionnelle), les résultats mis en avant sont les mêmes que précédemment : la différence n'est pas significative ce qui signifie que la réussite ou non du premier lancer franc n'a pas d'impact sur le résultat du second lancer franc (dans le tableau ci-dessous, P(H2/M1) signifie "probabilité de hit (tir réussi) après avoir raté le premier (miss)"). Afin de vérifier de nouveau le résultat, une étude a de plus été réalisée sur un panel de joueur de Cornell, pour qui ont été enregistrés les résultats d'une séance de 100 lancers francs. Et toujours pareil, aucun phénomène de main chaude en vue !
Cette idée reçue (et fallacieuse) d'existence de "main chaude" est reliée à l'illusion des séries, qui évoque la tendance à percevoir à tort des coïncidences dans des données au hasard à sous-estimer la variabilité des données. Dans le livre "Nudge", Richard Thaler, économiste de renom et théoricien de la finance comportementale, explique, je cite "It turns out that the "hot hands" is just a myth [...] To date, no one as found it".
Mais quel est le rapport avec l'économie ou la finance ? Le problème, pour reprendre R. Thaler, est que ce même type de biais cognitifs s'applique à de nombreux autres domaines, et que le relai par les médias tend à conforter à tort la population dans cette illusion des séries (les fameuses "vagues de suicide à France Télécom" par exemple --> lire "Pas de vague de suicides à France Télécom", selon un statisticien", même si une étude avec variables de contrôle pour l'âge et catégorie socio-professionnelle serait nécessaire). De plus, selon de nombreux modèles économiques, les agents sont supposés rationnels et doivent résoudre des problèmes complexes d'optimisation pour maximiser leur bien-être qui impliquent le calcul de la probabilité pour chaque espace d'état (fonction d'utilité de Von Neumannâ€Morgenstern). Une mauvaise capacité à estimer les probabilités d'un évènement implique donc une non-optimisation du bien-être et remet en cause le principe de rationalité (principe d'ailleurs remis en cause par la finance comportementale, en opposition à la théorie néoclassique).
Conclusion : (1) Acheter un ballon de basket, (2) ouvrir Excel, (3) trouver un panier, (4) réaliser 100 lancers francs et enregistrer tous vos résultats et (5) regarder la corrélation et la probabilité conditionnelle de vos lancers. Et vous verrez si effectivement vous avez "la main chaude" ou non (et si cela est significatif). En théorie, la réponse devrait être non, même si vous aurez peut-être eu cette impression durant votre série (la fameuse illusion des séries et la différence entre perception et réalité).
Cet article est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas de Modification 4.0 International. N'hésitez donc surtout pas à le voler pour le republier en ligne ou sur papier.
