La règle de Taylor et la politique monétaire

Présentée en 1993, la règle de Taylor (rien à voir avec le taylorisme au passage) a pour ambition de relier de manière assez simple la politique monétaire d'une banque centrale en fonction de l'inflation et de la croissance. Le taux d'intérêt nominal utilisé par les autorités monétaires est, selon la règle de Taylor, positivement corrélé à la différence entre l'inflation actuelle et la cible d'inflation, ainsi qu'à l'écart entre la croissance actuelle et la croissance potentielle. Pas de panique, on va reprendre ça tranquillement.

 

 En effet, lorsque le taux d'inflation actuel ou "anticipé" est supérieur à la cible d'inflation de la Banque Centrale (= inflation maximum tolérée par la banque centrale), alors, toutes choses égales par ailleurs, la Banque Centrale aura tendance à augmenter son taux d'intérêt pour tenter de contrôler l'inflation. En zone euro par exemple, si l'inflation se situe à un niveau supérieur à la cible de la BCE, à savoir au dessus de 2%, alors il y a fort à parier que la BCE relèvera ses taux (lire "Pourquoi la BCE a t-elle un objectif d'inflation de 2% ?"). Même raisonnement pour le différentiel de croissance: si la croissance actuelle (variation du PIB réel) est supérieur à la croissance potentielle (c'est-à-dire la variation du PIB maximale qui pourrait être réalisée grâce à la pleine utilisation des facteurs de production disponible), alors une Banque Centrale aura tendance, toutes choses égales par ailleurs, à augmenter les taux d'intérêt pour calmer les pressions inflationnistes et éviter une surchauffe de l'économie.

 

Actuellement, l'inflation est inférieure à la cible d'inflation de la BCE, et le PIB réel effectif des pays de la zone euro est bien inférieur au PIB potentiel (on dit alors que l'output gap est négatif). Les écarts d'inflation et de production sont donc négatifs, ce qui tend à faire baisser le taux directeur de la BCE. La règle de Taylor peut se formaliser de la manière suivante:

 

 

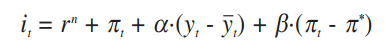
avec i_t le taux d'intérêt nominal fixé par la banque centrale, rⁿ le taux d'intérêt réel neutre, âˆ_t le taux d'inflation réel,  âˆ^* le taux d'inflation  cible, y_t le PIB réel, Ã¿_t le PIB potentiel. Nous avons montré précédemment pourquoi le taux d'intérêt nominal "i" est positivement relié à l'écart d'inflation et à l'output gap ; cela signifie donc simplement que l'on doit avoir des coefficients alpha et beta supérieurs à 0. Le taux d'intérêt réel neutre est égal, dans la règle de Taylor, au taux de croissance tendanciel de l'économie sur la période de référence (2% dans le cas des USA). Les coefficients alpha et beta sont, dans les premiers travaux de Taylor, fixés comme devant être égaux à 0,5. En supposant le taux d'inflation cible de la politique monétaire, cela nous donne donc:

 

 

 

Une augmentation de 1 point de l'inflation entraîne donc selon cette règle une hausse de 1,5 point du taux d'intérêt. A l'inverse, une hausse de 1 point de l'output gap (y - ÿ) tend à entraîner une hausse du taux d'intérêt de 0,5 point. 

 

Mais cette règle peut-elle être appliquée à la réalité ? Si l'on regarde sur la période d'étude sur laquelle Taylor a réalisée ses tests (de 1987 à 1992), alors cette règle répliquait assez bien la politique monétaire de la Federal Reserve américaine. Mais les résultats sont très sensibles au choix des coefficients alpha et beta de notre équation, qui ont été fixés par Taylor à 0,50 mais sans réelle justification économique. De plus, il existe un décalage entre le moment où sont publiés les chiffres de nos variables explicatives (inflation et croissance) et notre variable dépendante (le taux d'intérêt) qui est une variable financière disponible en temps réel. L'inflation est en effet publiée avec un retard d'une quinzaine de jours (l'inflation d'octobre sera publiée le 14 novembre) et le PIB n'est publié que trimestriellement, avec un retard de 45 jours (le PIB du troisième trimestre 2012 "juillet-août-septembre" sera publié le 15 novembre). Pour juger d'un point de vue normatif la règle de Taylor, il faut donc utiliser des prévisions (type inflation anticipée et prévisions de croissance), avec les incertitudes que cela engendre nécessairement.

 

Cela dit, certaines études économétriques montrent comment avec quelques petits ajustements et sans restriction sur les coefficients, il est possible d'adapter la règle de Taylor pour décrire avec une très bonne précision l'évolution du taux directeur de la FED sur une longue période. L'étude "Monetary policy inertia: fact or fiction?" de Glenn Rudebusch (qui n'est autre que l'actuel directeur de la recherche économique de la FED) démontre cela, en comparant le taux réel de la FED au taux estimé selon une règle de Taylor modifiée. L'écart très faible entre le taux directeur de la FED et l'estimation de ce taux en utilisant une règle de Taylor montre donc l'applicabilité de cette règle dans un but descriptif. Les coefficients alpha et beta sont ici estimés économétriquement, justement afin que le taux estimé "fitted value" soit le plus proche possible du taux réel "actual value". Rudebusch remarque ainsi que dans le cas de la politique monétaire de la FED et sur la période d'étude 1988-2004, les coefficients estimés ne sont pas exactement ceux définis par Taylor (alpha = 1,39 et beta = 0,92 dans l'étude économétrique de Rudebusch ; contre alpha = 1,5 et beta = 0,5 dans le règle initiale de Taylor).

 

 

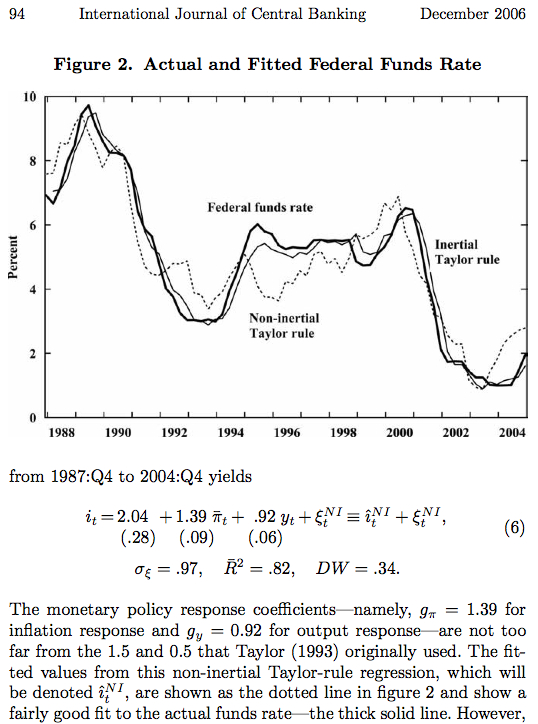
Dans le cas français, une étude de la Banque de France intitulée "Règle de Taylor : présentation, application et limites" démontre que les résultats de l'application de la règle de Taylor stricte au cas français ne sont pas concluants. C'est à dire qu'en utilisant les coefficients "arbitraires" de 0,5 pour alpha et beta et les variables définies dans le modèle initial de Taylor en 1993, il n'est pas possible de retracer avec précision la politique monétaire française.

 

Il faut bien différencier le caractère descriptif de la règle de Taylor, ayant pour but de comprendre les décisions passées d'une Banque Centrale, du caractère normatif de la règle, pouvant servir à anticiper et prévoir les variations futures de la politique monétaire. Pour que la règle puisse avoir un caractère normatif, il faut en effet que le comportement historique de la Banque Centrale soit le même que son comportement futur, ce qui implique une stabilité des coefficients et des variables explicatives. De plus, chaque Banque Centrale ayant ses propres objectifs et la situation économique de chaque pays étant différente, chaque pays aura sa propre règle de Taylor, avec des coefficients et/ou des variables explicatives différentes. Bref, le Captain' trouve la règle de Taylor très intéressante pour estimer les variations passées et mieux comprendre la politique monétaire historique d'un pays, mais doute fortement de l'applicabilité de cette règle pour prévoir avec précision la politique monétaire à venir d'une banque centrale.

 

Conclusion: La règle de Taylor permet de comprendre simplement le lien entre inflation, croissance et taux d'intérêt. Résumons donc la politique monétaire probable d'une banque centrale, toutes choses égales par ailleurs : (1) si l'inflation actuelle ou anticipée est supérieure à la cible d'inflation, on monte les taux, (2) si l'inflation actuelle ou anticipée est inférieure à la cible d'inflation, on diminue les taux, (3) si la croissance actuelle est supérieure à la croissance potentielle, on monte les taux et (4) si la croissance actuelle est inférieure à la croissance potentielle, on diminue les taux. La situation se complique si par exemple l'inflation est supérieure à la cible mais que dans le même temps la croissance est bien en dessous de la croissance potentielle (cas de stagflation). En effet dans ce cas là, si la banque centrale augmente ses taux, alors l'inflation va diminuer, certes, mais cela va agrandir davantage encore l'écart entre la croissance actuelle et la croissance potentielle (car hausse de taux  = baisse investissement = baisse croissance actuelle = élargissement de l'output gap).