Après avoir vu la semaine dernière le principe de l'"Optimisation sous contrainte et le multiplicateur de Lagrange", avec une interprétation intuitive et graphique de la façon dont un consommateur essaye à chaque instant de maximiser son bien-être sous contrainte budgétaire, nous allons commencer la semaine par un peu de maths, en apprenant comment résoudre techniquement ce genre de problème avec la méthode du Lagrangien.
La méthode du Lagrangien permet de résoudre les problèmes d'optimisation de fonction sous contrainte. Le principe général est finalement assez simple. Souvenez-vous du temps où vous vous amusiez comme un petit fou au lycée à faire des études de fonctions... On vous donnait alors une fonction, du type f(x) = 5 - 10x + x2 , et vous deviez analyser cette fonction, en réalisant un beau tableau de variations et en indiquant les valeurs stationnaires (minimum et maximum local de votre fonction). Comment faisiez-vous pour arriver à cela ? Et bien vous calculiez la dérivé de votre fonction, f'(x), et vous regardiez les valeurs pour lesquelles f'(x) = 0. Ãa vous rappelle quelque chose ?
Un problème d'optimisation en économie est assez similaire à cela : le but étant aussi de déterminer les points stationnaires (minimum, maximum) d'une fonction de bien-être ou de profits (par exemple). Mais à la différence du cas simple présenté précédemment, cette optimisation doit se faire en respectant une certaine contrainte, par exemple une contrainte budgétaire dans le cadre d'un consommateur (budget maximum). Vous n'allez donc plus devoir maximiser une fonction simple à une seule variable, mais une fonction du type f(x,y) = âx * ây , sous la contrainte que 3x + 4y = 24. En traduisant cela de manière économique, vous allez essayer de maximiser votre fonction d'utilité f(x,y), qui dépend de la quantité consommée du bien x et de la quantité consommée du bien y, tout en respectant votre contrainte budgétaire de 24 euros (le bien X coûtant 3 euros et le bien Y 4 euros dans notre exemple).
Pour résoudre cela, il faut donc dans un premier temps poser la fonction du Lagrangien L(x , y , λ) = f(X) - λ * h(x) ; avec f(X) la fonction a optimiser et h(X) la contrainte à respecter, tel que h(X) = 0. Dans notre exemple, le Lagrangien s'écrit donc L(x , y , λ) = âx * ây - λ [24 - 3x - 4y]. En posant donc un Lagrangien à la place d'une fonction à optimiser ET d'une contrainte, on se retrouve alors dans un problème de recherche de points stationnaires d'une fonction à 3 variables sans contrainte. Et pour trouver les valeurs de x*, y* et λ* permettant de résoudre notre problème, il faut donc trouver les valeurs annulant chacune des dérivés partielles de premier ordre, c'est à dire un système tel que :
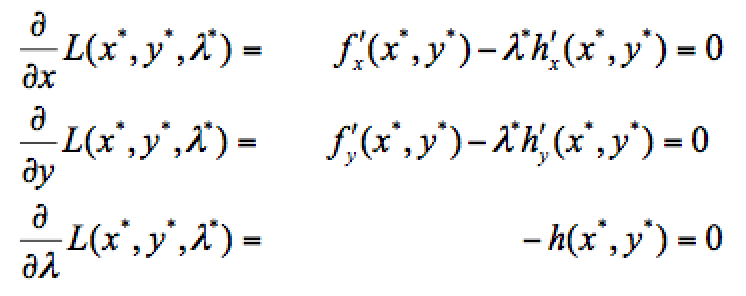
Dans notre exemple, cela nous donne donc le système suivant (pour rappel, la dérivée d'une fonction f(x) = âx est f'(x) = (1 / 2âx)) :
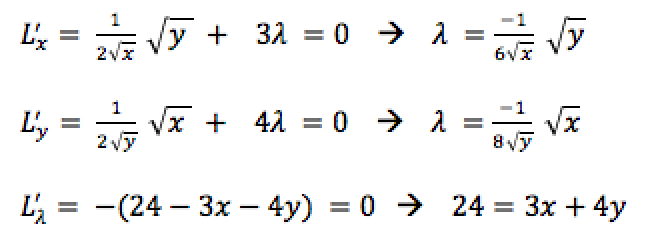
La dernière dérivée partielle correspond exactement à notre contrainte, et l'utilisation des deux premières dérivées partielles va nous permettre d'exprimer "x" en fonction de "y", puis de trouver les valeurs optimales en réinjectant cela dans notre contrainte.
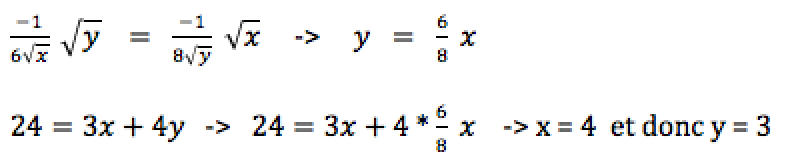
Et voilà , c'est terminé. Pour maximiser son bien-être (sa fonction d'utilité), notre consommateur doit donc consommer 4 unités du bien X, et 3 unités du bien Y. Assez simple, non ?
Conclusion: Pour plus d'informations sur le multiplicateur de Lagrange et une application au cas du producteur, le Captain' vous conseille de lire le cours de Licence 3 de l'Universite de Nanterre disponible gratuitement en ligne sur le site Economix (source: "Rappels sur la méthode dâ€optimisation du Lagrangien").
Cet article est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas de Modification 4.0 International. N'hésitez donc surtout pas à le voler pour le republier en ligne ou sur papier.
