Moyenne géométrique et moyenne arithmétique : calcul de rendement

Le Captain' vous propose aujourd'hui un super deal : si vous achetez aujourd'hui des actions de l'entreprise XYZ, le Captain vous garanti les rendements suivants: +50 % la première semaine et -40% la seconde. Pas mal non, un gain moyen de 5% par semaine ? Pas mal comme arnaque surtout ! En effet, dans cet exemple, si vous placez 1000 euros dans l'entreprise XYZ, votre investissement aura à la fin de la 1ère semaine une valeur totale de 1500 euros (1000 euros * (1 + 50%)), mais à la fin de la seconde semaine, votre portefeuille aura une valeur totale de seulement 900 euros (1500 euros * (1 - 40%)), soit une valeur inférieure à sa valeur d'origine. Voici un simple exemple montrant pourquoi il ne faut surtout pas utiliser la moyenne arithmétique (somme des rendements divisé par le nombre de périodes) lorsque vous souhaitez voir le rendement d'un portefeuille sur plusieurs périodes. Mais alors, que faut-il utiliser ?

 

 C'est finalement assez simple. Dans notre exemple ci-dessous, la première année, la valeur votre portefeuille a été multipliée par 1,5 (1 + 50% = 1,5), et la seconde année par 0,6 (1 - 40% = 0,6). Afin de calculer le rendement annuel moyen, la formule à utiliser est ce que l'on appelle la moyenne géométrique, qui est égale à la racine n-ième (n étant le nombre de période) de la multiplication des rendements, auquel on retranche 1. Whaaaaat ? Dans notre exemple, nous avons (1) n = 2 (deux périodes) et (2) un portefeuille mutliplié par 1,5 à la première période puis multiplié par 0,6 à la seconde. On multiplie alors 1,5 par 0,6, ce qui nous donne 0,9 ; ensuite, on prend la racine carré (car deux périodes) de 0,9 (=0,948) auquel on retranche 1 ----> et voilà donc notre rendement moyen par période de -5,2%.

 

En appliquant ce rendement moyen par période, cela signifie en lissant les rendements qu'à la fin de la 1ère semaine, votre portefeuille aura une valeur de 1000 * (1 - 5,2%) = 948,7 euros, et à la fin de la seconde de 948,7 euros * (1 - 5,2%) = 900 euros. On retrouve alors bien notre "900 euros" de l'introduction, mais au lieu d'un rendement par période calculé via la moyenne arithmétique de +5% (50% - 40% divisé par 2), le rendement réel, calculé via la moyenne géométrique est de -5,2%. Cela fait tout de même une belle petite différence.

 

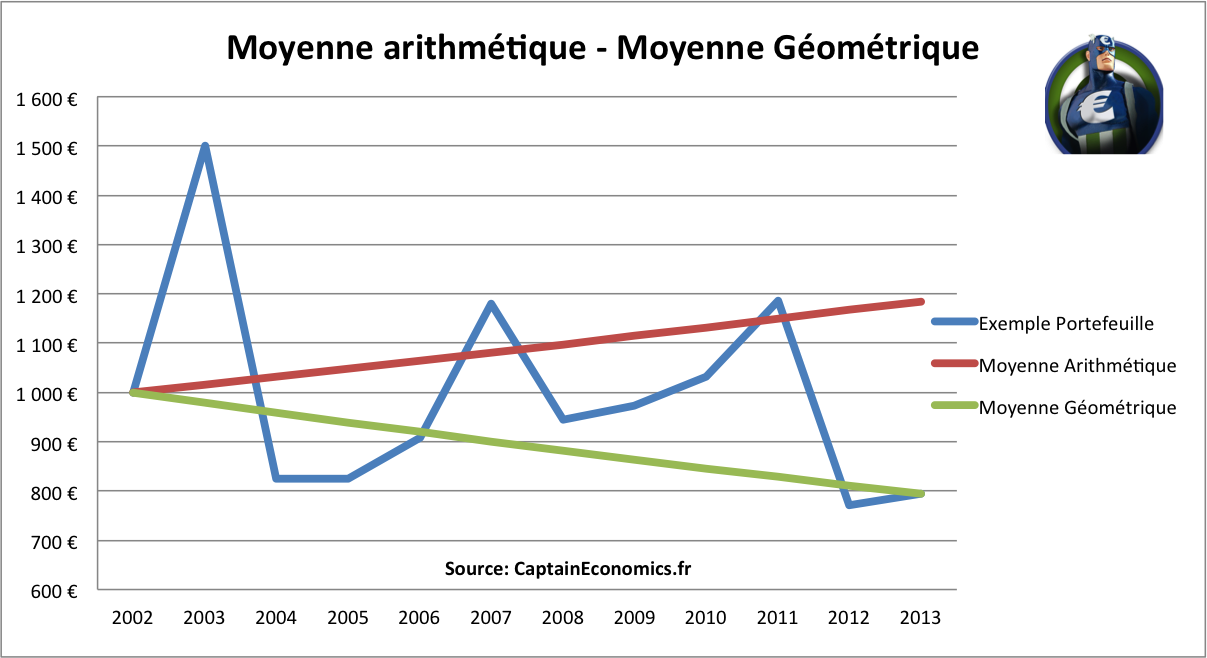
Prenons un deuxième exemple rapide. Supposons que l'on vous donne le tableau ci-dessous, avec le rendement annuel d'un portefeuille entre 2003 et 2013. En 2003, votre portefeuille a donc gagné 50%, puis perdu 45% en 2004, etc... Si l'on considère la moyenne arithmétique des rendements (moyenne "classique"), on arrive donc à +1,55% par an. En suivant la moyenne arithmétique, 1000 euros investi en 2003 vaudrait au final 1185 euros.

 

Mais en réalité, si l'on applique les variations de ce portefeuille en considérant l'évolution année par année d'un investissement initial de 1000 euros, on se rend compte que fin 2013, votre portefeuille ne vaut plus que 794 euros. Et l'on arrive bien évidemment au même chiffre en calculant la moyenne géométrique, avec un rendement annuel moyen de -2,07%.

 

 

 

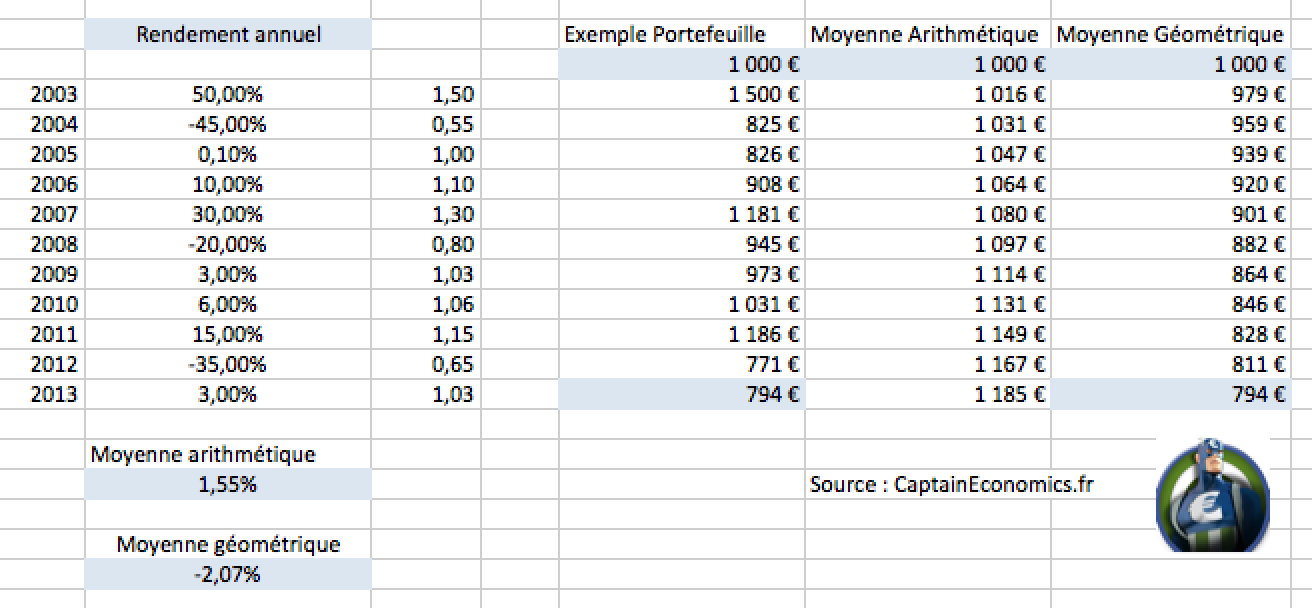
Sur Excel, vous pouvez calculer simplement la moyenne géométrique via la fonction "MOYENNE.GEOMETRIQUE()" ou "GEOMEAN()" en anglais. Pour le calculer à la main, voici donc la formule : 

 

 

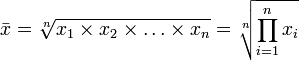
Pour éviter le problème en cas de valeur négative, considérer les variables "x" comme la valeur de multiplication via le rendement ; par exemple un rendement de +20% correspond à une valeur de 1,20. Ensuite, il vous suffit de retrancher 1 à la formule ci-dessous pour retrouver le rendement moyen par période de votre portefeuille.

 

Conclusion : Ne jamais prendre la moyenne arithmétique pour un calcul avec des taux de variations sur plusieurs périodes (idem pour la croissance moyenne du PIB, le taux moyen d'inflation sur x périodes) ! Sauf si vous êtes SM et que vous aimez vous prendre des coups de règles sur les doigts, mais dans ce cas le Captain' ne peut pas faire grand chose pour vous...